CARATTERI PER IL DISEGNO TECNICO
_________________________________________________________________________________
METODI DI RAPPRESENTAZIONE
DI OGGETTI 3D
SU SUPPORTO BIDIMENSIONALE (FOGLIO DA DISEGNO)
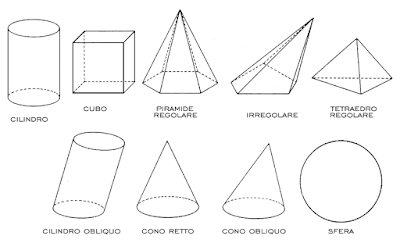
I SOLIDI E LA LORO RAPPRESENTAZIONE SUL PIANO
ASSONOMETRIE (axonometry, axonométrie)
LINK: ASSONOMETRIE, PROIEZIONI ORTOGONALI E PROSPETTIVA
LINK: L’axonométrie et la représentation conceptuelle
LINK: axonometry projection
LINK: L’axonométrie et la représentation conceptuelle
LINK: axonometry projection
ASSONOMETRIA MONOMETRICA
ASSONOMETRIA ISOMETRICA
ASSONOMETRIA CAVALIERA
______________________________________________________________________
SVILUPPO DI SOLIDI
SVILUPPO DI UN PARALLELEPIPEDO
_________________________________________________________________________________TttTAVOLA 1:
PROIEZIONE ORTOGONALE DEL CUBO DI RUBIK
TAVOLA 2
TAVOLA 3
TAVOLA 4:
ASSONOMETRIA CAVALIERA DEL CUBO DI RUBIK
TAVOLA 5
TAVOLA 6: FRONTE
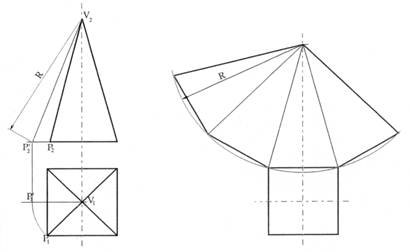
PROIEZIONE ORTOGONALE DI UNA PIRAMIDE A BASE QUADRATA
(DIMENSIONI A PIACERE)
TAVOLA 6: RETRO DEL FOGLIO
SVILUPPO SUL PIANO DI UNA PIRAMIDE A BASE QUADRATA
(STESSE DIMENSIONI)
TAVOLA 7: FRONTE
PROIEZIONE ORTOGONALE DEL DIARIO IN SCALA 1:3
TAVOLA 7: RETRO DEL FOGLIO (SQUADRATURA A MANO)
ASSONOMETRIE E SVILUPPO DI UN PARALLELEPIPEDO
TAVOLA 8
TAVOLA 9: FRONTE
PROIEZIONE ORTOGONALE DI UN PRISMA A BASE TRIANGOLARE
(DIMENSIONI A PIACERE)
TAVOLA 9: RETRO DEL FOGLIO
ASSONOMETRIA ISOMETRICA E SVILUPPO
ASSONOMETRIA ISOMETRICA E SVILUPPO
DI UN PRISMA A BASE TRIANGOLARE
TAVOLA 10
TAVOLA 11
TAVOLA 12
TAVOLA 13
Costruiamo il TETRAEDRO...
e scopriamo il teorema di Pitagora
TAVOLA 14: ASSONOMETRIA MONOMETRICA E SVILUPPO
DI UN TETRAEDRO REGOLARE DI LATO 3
mettiamo il foglio in orizzontale e lo dividiamo in due parti: a sinistra disegnamo l'assonometria monometrica e a destra lo sviluppo (ricordando che tutte le facce sono triangoli equilateri e si costruiscono a partire dal lato di base utilizzando il compasso )
COME RICAVO L'ALTEZZA DEL TETRAEDRO PER REALIZZARE L'ASSONOMETRIA:
costruisco un triangolo equilatero di lato 12 cm e trovo l'altezza VO con metodo grafico
(divido il risultato ottenuto per 4 poiché il lato del tetraedro da disegnare è 3cm ovvero 1/4 del lato che ho usato per ricavare l'altezza)
scopro così che sommando le misure dei cateti elevate al quadrato ottengo lo stesso valore che otterrei elevando al quadrato l'ipotenusa.
In altre parole:
LA SOMMA DELLE AREE DEI QUADRATI COSTRUITI SUI CATETI
EQUIVALE A QUELLA DEL QUADRATO COSTRUITO SULL'IPOTENUSA.
Questo, in matematica, prende il nome di Teorema di Pitagora.
Potrò quindi calcolare numericamente il valore preciso dell'altezza del tetraedro utilizzando il teorema di Pitagora:
________________________________________________________________________________
TAVOLA 15: ASSONOMETRIA ISOMETRICA DI MURATURE
(disegno di Alice)
TAVOLA 16
Assonometria isometrica di una piramide a base esagonale.
(disegno di Federica)
Tavola 17







.jpg)